What is a Koch curve?
A Koch curve (alternatively Koch snowflake) is a curve that contains multiple layers of folds inside of even more folds. It resembles patterns often seen in nature such as, coastlines and snowflakes. The result is an aesthetic complex shape that pairs nicely with computer graphics.
A Koch curve is a part of the field in mathematics known as 'fractal geometry'. The field was popularised by mathematician Benoit Mandelbrot (commonly referred to as the father of fractal geometry). Although Mandelbrot is quite famous for his discoveries, earlier mathematicians had found similar mathematical properties, but they found them to be quite strange and difficult to reason about. This gave rise the field being labelled as "mathematical monsters" by early mathematicians (Gaddis and Zyda).
Fractal geometry is broad field. There exists many types of fractals, some well-known ones being, the Sierpinski triangle, the Cantor set, and the famous, Mandelbrot set.
Requirements:
We will be using raylib a C based graphics library.
Getting Started
Once raylib is installed create a directory called fractal. Insert a file main.c into the project's root directory.
If you are using a Unix-like operating system this can be done by doing:
mkdir fractal
cd fractal
touch main.c
To speed up our work we will borrow some boilerplate from raylib's example page.
/*******************************************************************************************
*
* raylib [core] example - Basic window
*
* Example licensed under an unmodified zlib/libpng license, which is an OSI-certified,
* BSD-like license that allows static linking with closed source software
*
* Copyright (c) 2013-2024 Ramon Santamaria (@raysan5)
*
********************************************************************************************/
#include "raylib.h"
// Program main entry point
//------------------------------------------------------------------------------------
int main(void)
{
// Initialization
const int screenWidth = 800;
const int screenHeight = 450;
InitWindow(screenWidth, screenHeight, "raylib [core] example - basic window");
SetTargetFPS(60); // Set our game to run at 60 frames-per-second
// Main game loop
while (!WindowShouldClose()) // Detect window close button or ESC key
{
// Update
//----------------------------------------------------------------------------------
// Draw
BeginDrawing();
ClearBackground(RAYWHITE);
DrawText("Congrats! You created your first window!", 190, 200, 20, LIGHTGRAY);
EndDrawing();
//----------------------------------------------------------------------------------
}
// De-Initialization
CloseWindow(); // Close window and OpenGL context
return 0;
}
After running the program you should see this output:
If you managed to get the above image, congratulations you ran your first raylib program, but our work is not done. Next, we will use our boilerplate code to generate the Koch curve.
Koch curve
We will be utilizing math functions, so it is necessary to include a <math.h> header file at the top of the file. Additionally we will need the irrational number PI as shown below. Add the following lines to the top of the file right below #include "raylib.h"
#include <math.h>
#define pi M_PI
Next, define a global struct point that holds x and y coordinates.
typedef struct {
double x, y;
} point
Now we will define the kochCurve() function which will be called recursively. The return type will be void. The function will take in 3 arguments: a point p1, a point p2, and an int folds. Points p1 and p2 are used to draw the "initiator", a straight the line, folds is used to determine the number of times the recursion is called. The function will look like this:
void kochCurve(point p1, point p2, int folds)
Inside our function kochCurve() declare three points as local variables p3, p4, and p5. These points will represent our "generator". Also define a double theta to be PI divided by 3. An explanation of the generator will be given later.
point p3, p4, p5;
double theta = pi / 3;
As previously mentioned an initiator is a straight line. More important is the generator, which is the result of taking the initiator dividing it into three equal parts and inserting into into it an equilateral triangle without a base. As shown below:
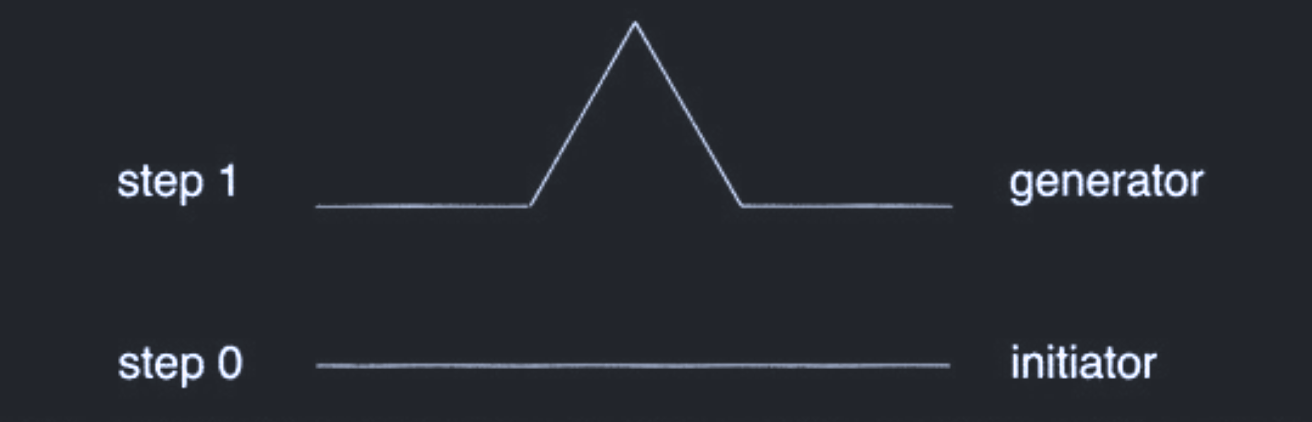
For the main bulk of the Kochcurve function begin by writing a conditional that will return true if (fold > 0). With this our recursion will be able to terminate when this condition is false. Inside the conditional we will set points p3, p4 and p5 these points will calculate the generator, our equilateral triangle with the base removed. Then, we call the recursion Kochcurve four times making sure to subtract 1 from folds in each call. Finally if our condtion is false use raylib's DrawLine() function to all the lines. Include BLACK as the last argument available through raylib. Our final koch curve. Your function should look like this:
void kochCurve(point p1, point p2, int folds) {
point p3, p4, p5;
double theta = pi / 3;
if (folds > 0) {
p3 = (point){(2 * p1.x + p2.x) / 3, (2 * p1.y + p2.y) / 3};
p5 = (point){(2 * p2.x + p1.x) / 3, (2 * p2.y + p1.y) / 3};
p4 =
(point){p3.x + (p5.x - p3.x) * cos(theta) + (p5.y - p3.y) * sin(theta),
p3.y - (p5.x - p3.x) * sin(theta) + (p5.y - p3.y) * cos(theta)};
kochCurve(p1, p3, folds - 1);
kochCurve(p3, p4, folds - 1);
kochCurve(p4, p5, folds - 1);
kochCurve(p5, p2, folds - 1);
}
else {
DrawLine(p1.x, p1.y, p2.x, p2.y, BLACK);
}
}
All that is left is our main function.
Declare p1, p2, and folds below the variables screenWidth and screenHeight. The loop while (!WindowShouldClose()) is our main loop. Inside it define p1 = (point){0, screenHeight - 0} and p2 = (point){screenWidth - 0, screenHeight - 0}. Replace the DrawText("Congrats! You created your first window!", 190, 200, 20, LIGHTGRAY); with Kochcurve(p1, p2, folds). Here is our main function.
int main() {
const int screenWidth = 800;
const int screenHeight = 450;
// Kosch Initialization
point p1, p2;
int folds;
// Screen Initialization
InitWindow(screenWidth, screenHeight, "raylib [core] example - basic window");
SetTargetFPS(1); // Set our game to run at 60 frames-per-second
// Main game loop
while (!WindowShouldClose()) // Detect window close button or ESC key
{
if (IsKeyPressed(KEY_S)) {
TakeScreenshot("screenshot.png");
// Be sure to not place this function inside a loop where
// it saves a screenshot every frame!
}
p1 = (point){0, screenHeight - 0};
p2 = (point){screenWidth - 0, screenHeight - 0};
if(folds < 10){
folds = folds + 1;
}
// Update
BeginDrawing();
ClearBackground(RAYWHITE);
kochCurve(p1, p2, folds);
EndDrawing();
}
// De-Initialization
CloseWindow(); // Close window and OpenGL context
return 0;
}
Final Code
#include "raylib.h"
#include <math.h>
#define pi M_PI
typedef struct {
double x, y;
} point;
void kochCurve(point p1, point p2, int folds) {
point p3, p4, p5;
double theta = pi / 3;
if (folds > 0) {
p3 = (point){(2 * p1.x + p2.x) / 3, (2 * p1.y + p2.y) / 3};
p5 = (point){(2 * p2.x + p1.x) / 3, (2 * p2.y + p1.y) / 3};
p4 =
(point){p3.x + (p5.x - p3.x) * cos(theta) + (p5.y - p3.y) * sin(theta),
p3.y - (p5.x - p3.x) * sin(theta) + (p5.y - p3.y) * cos(theta)};
kochCurve(p1, p3, folds - 1);
kochCurve(p3, p4, folds - 1);
kochCurve(p4, p5, folds - 1);
kochCurve(p5, p2, folds - 1);
}
else {
DrawLine(p1.x, p1.y, p2.x, p2.y, BLACK);
}
}
int main() {
const int screenWidth = 800;
const int screenHeight = 450;
// Kosch Initialization
point p1, p2;
int folds;
// Screen Initialization
InitWindow(screenWidth, screenHeight, "raylib [core] example - basic window");
SetTargetFPS(1); // Set our game to run at 60 frames-per-second
// Main game loop
while (!WindowShouldClose()) // Detect window close button or ESC key
{
if (IsKeyPressed(KEY_S)) {
TakeScreenshot("kochcurve.png");
// Be sure to not place this function inside a loop where
// it saves a screenshot every frame!
}
p1 = (point){0, screenHeight - 0};
p2 = (point){screenWidth - 0, screenHeight - 0};
if(folds < 10){
folds = folds + 1;
}
// Update
BeginDrawing();
ClearBackground(RAYWHITE);
kochCurve(p1, p2, folds);
EndDrawing();
}
// De-Initialization
CloseWindow(); // Close window and OpenGL context
return 0;
}
Result
To take a screenshot press S on your keyboard, while the program is running. You should see kochcurve.png in your project's root directory.
The final result:
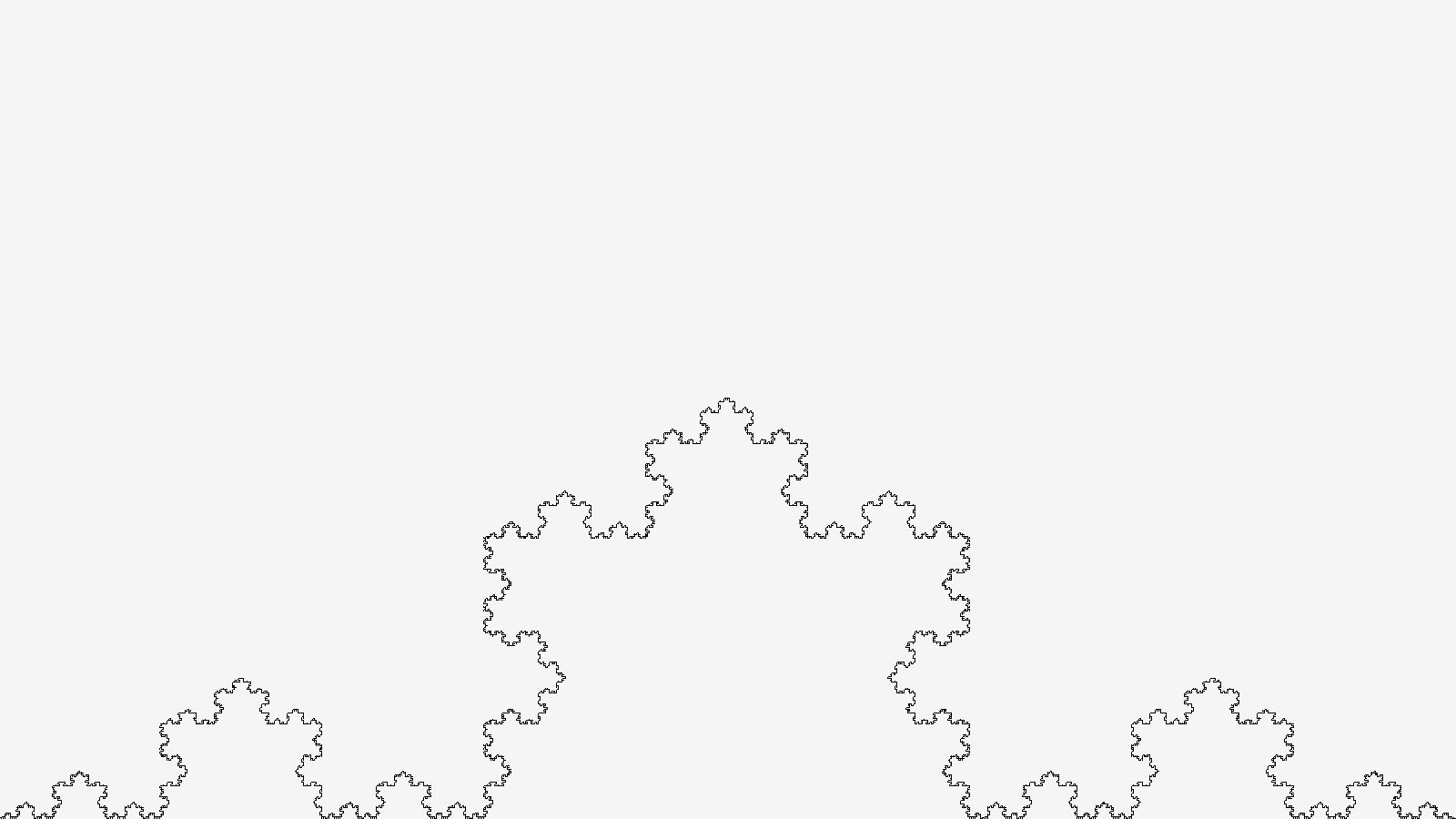
Voila! You have now created a Koch Curve in C using raylib. Feel Free to mess around with the code and see what you can come up with.
Full code available here
References
Peitgen, Heinz-Otto, et al. Chaos and fractals: new frontiers of science. Vol. 106. New York: Springer, 2004.
Gaddis, Michael E., and Michael J. Zyda. The Fractal Geometry of Nature: Its Mathematical Basis and Application to Computer Graphics. Naval Postgraduate School, 1986.
“Koch Curve.” Rosetta Code, 15 Apr. 2024, https://rosettacode.org/wiki/Koch_curve.
Fractal Geometry. https://users.math.yale.edu/public_html/People/frame/Fractals/.